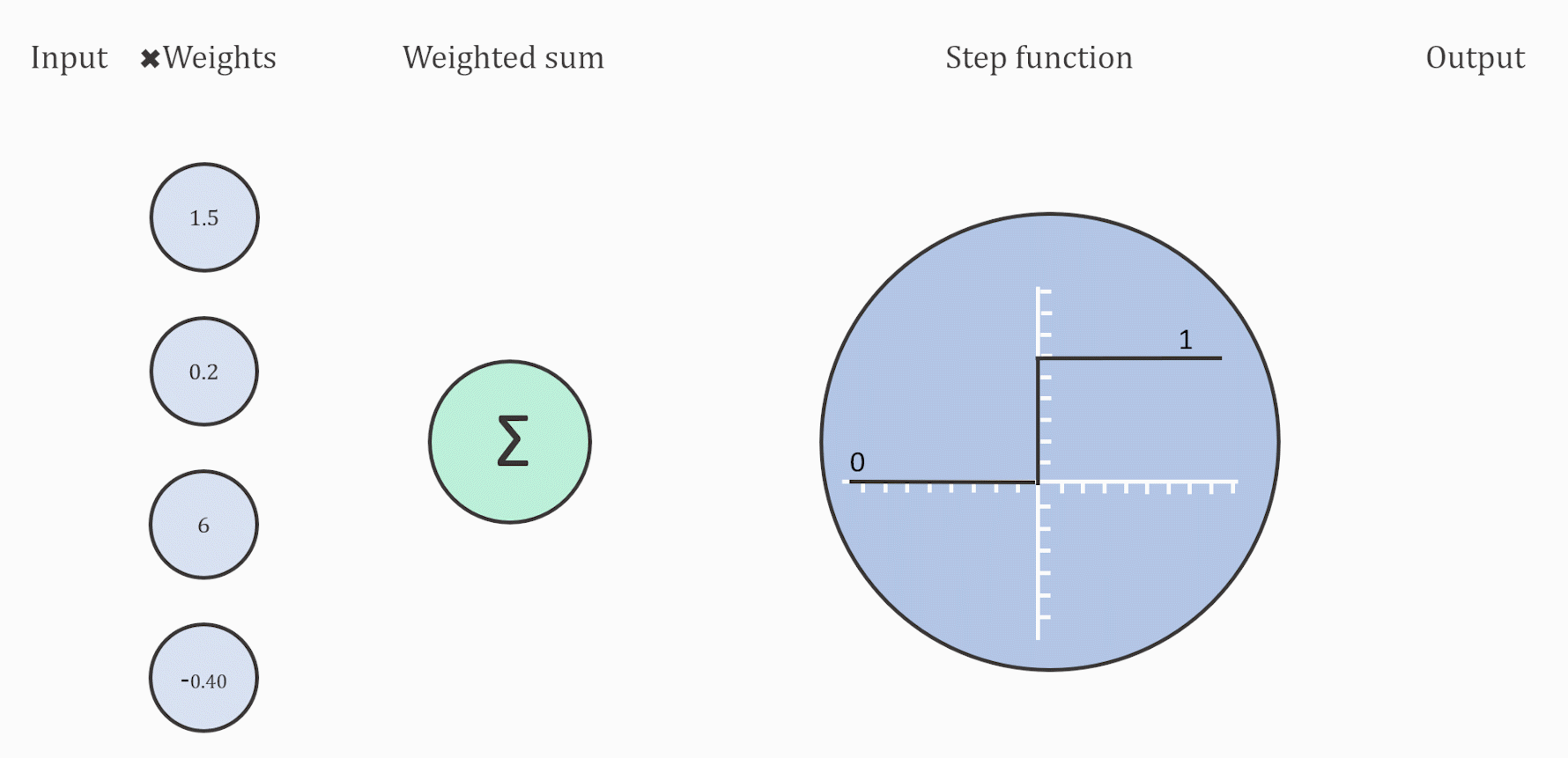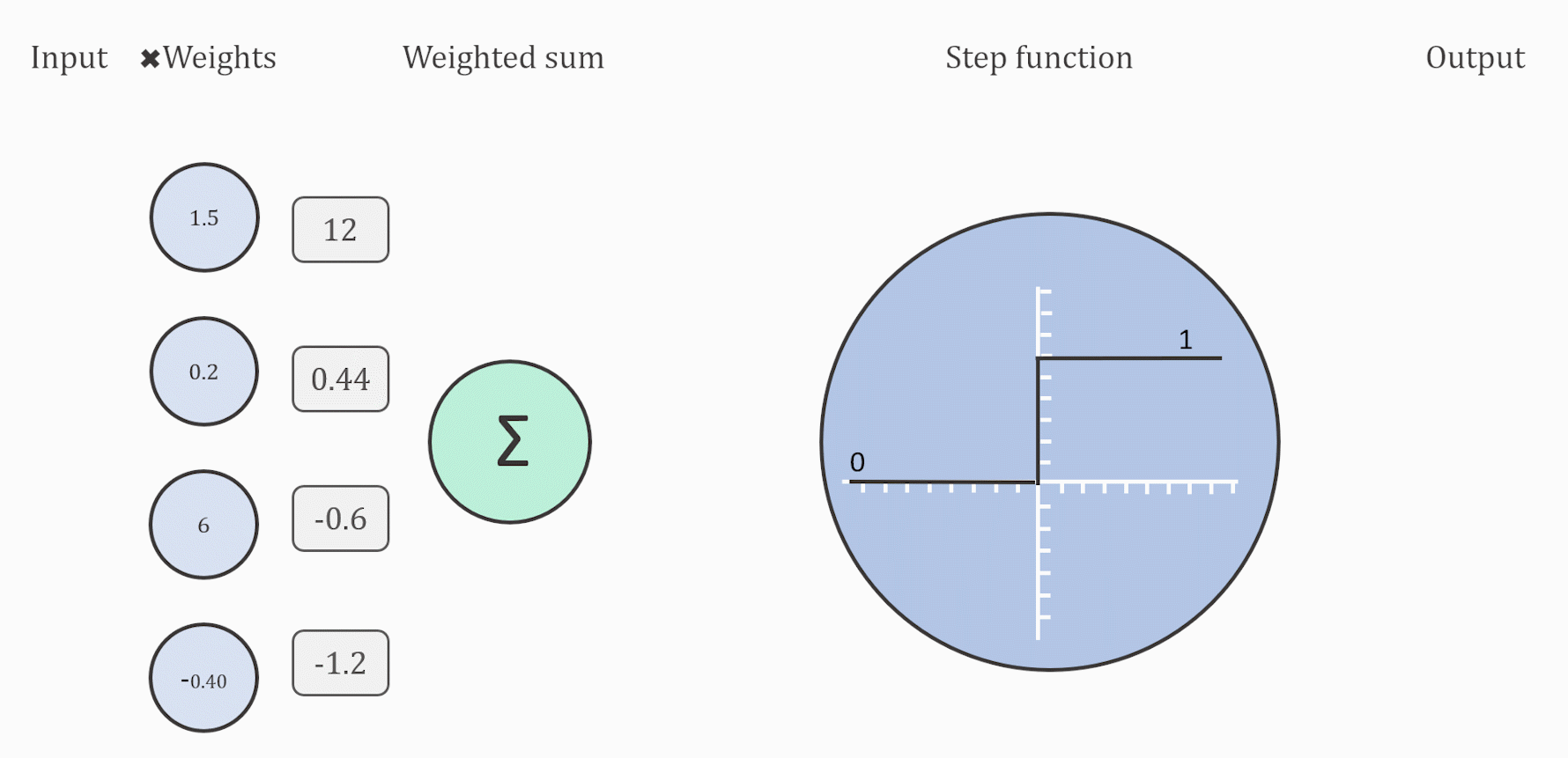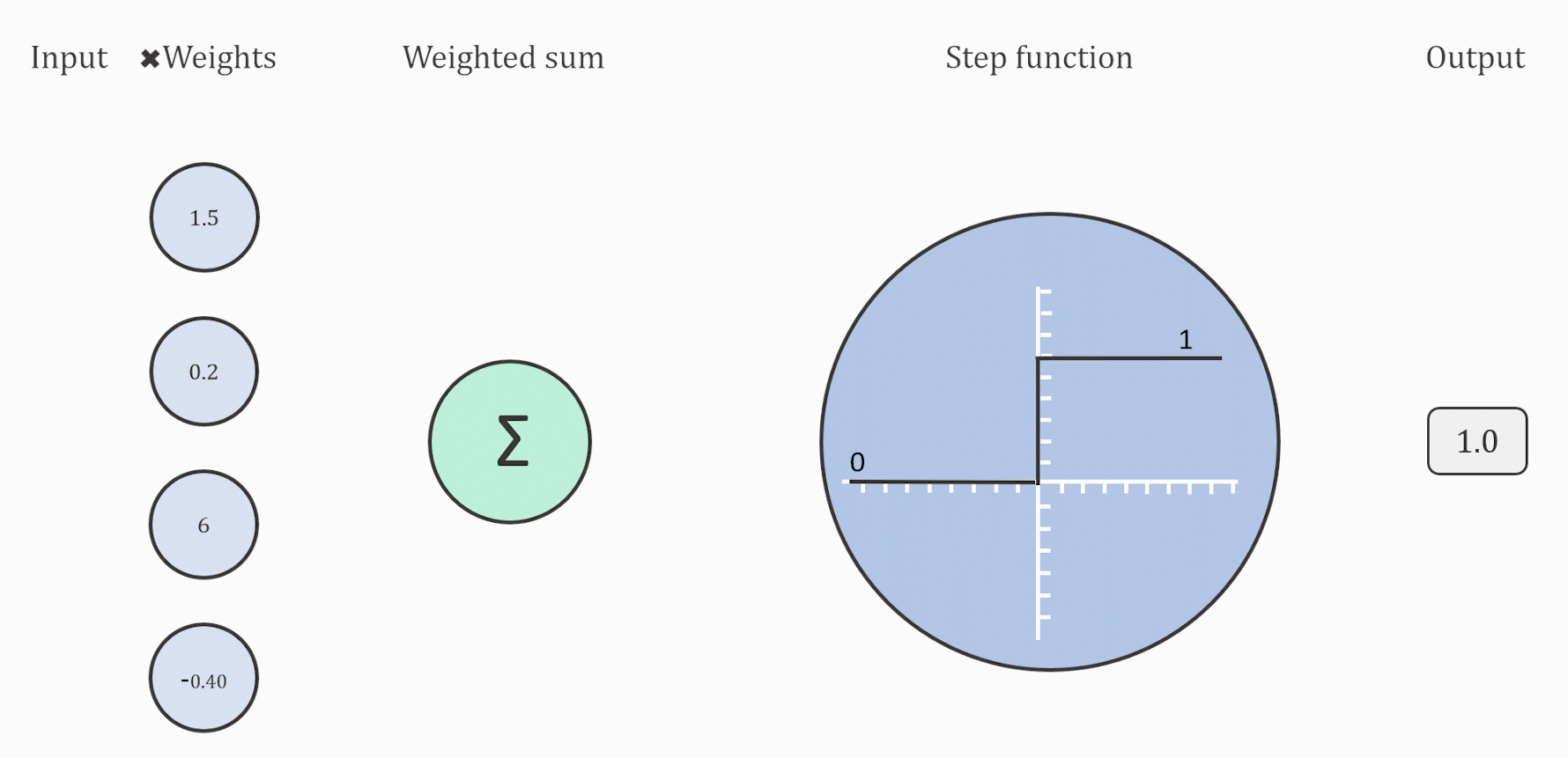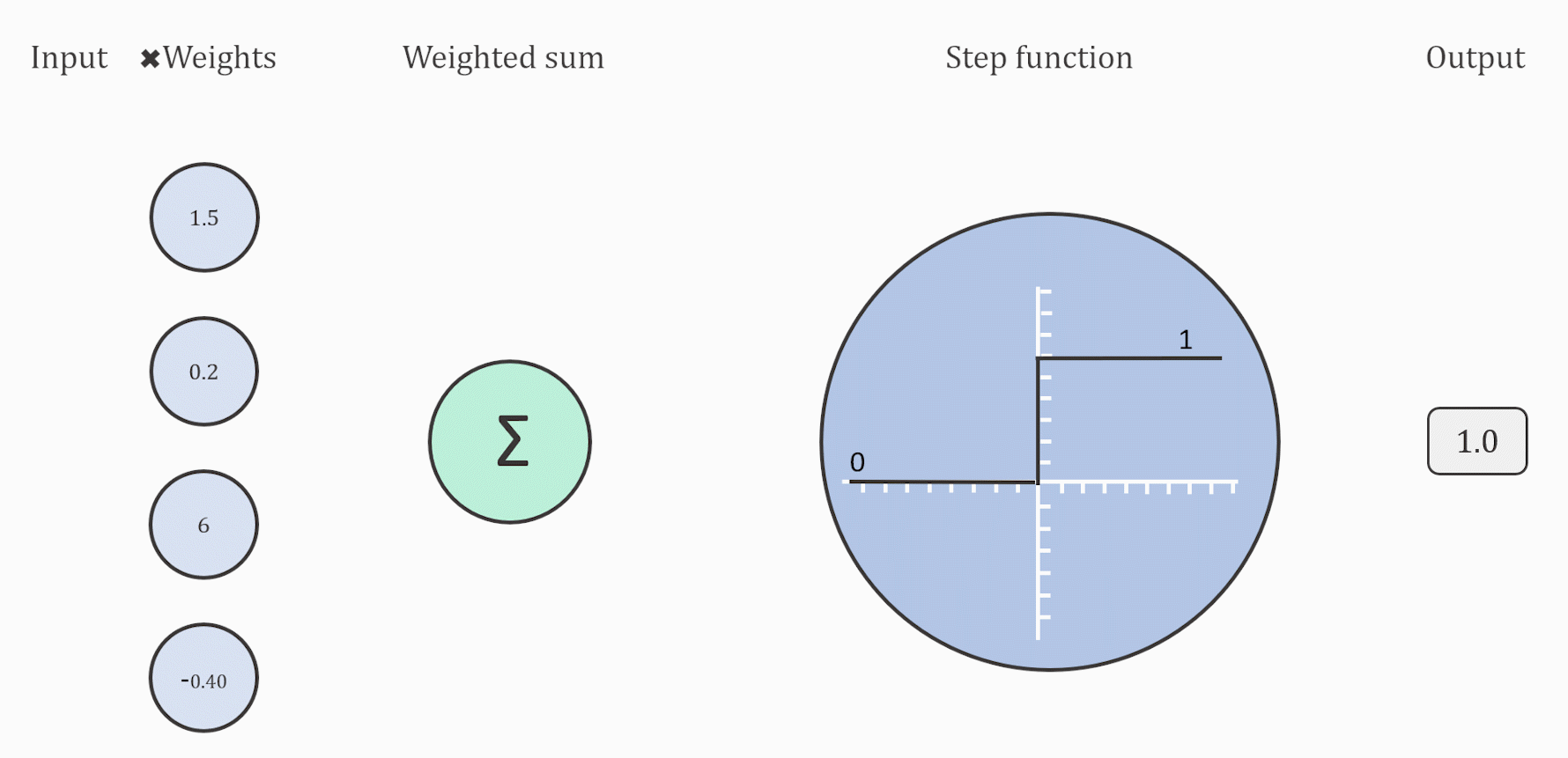
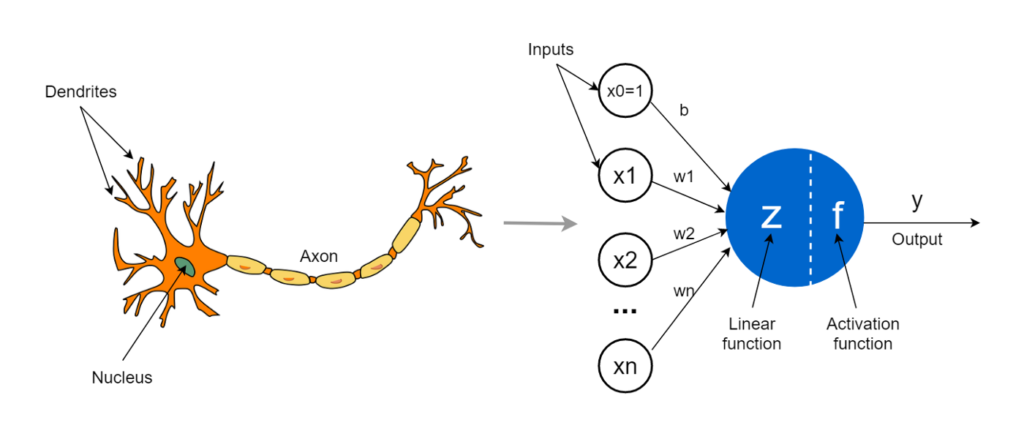
به بیان ساده، تابع فعال سازی تابعی است که به شبکه عصبی مصنوعی اضافه میشود تا به شبکه کمک کند الگوهای پیچیده در دادهها را یاد بگیرد. هنگام مقایسه با یک مدل مبتنی بر نورون که در مغز ما وجود دارد، عملکرد تابع فعال سازی در پایان تصمیم میگیرد که چه چیزی به نورون بعدی انتقال داده شود و چه چیزی نه. این دقیقاً همان کاری است که یک تابع فعال سازی در ANN نیز انجام میدهد. سیگنال خروجی سلول قبلی را میگیرد و آن را به شکلی تبدیل میکند که میتواند به عنوان ورودی به سلول بعدی گرفته شود. مقایسه این مفهوم را میتوان در شکل زیر خلاصه کرد. برای کسب مهارت در انتخاب تابع فعالسازی مناسب ابتدا باید کاربرد و عملکرد آن را درک کنید. در این مطلب مروری بر تاریخچهی تابع فعالسازی، ویژگیهای آن و در نهایت کاربردهای تابع فعالسازی در شبکه عصبی خواهیم داشت.
فهرست مطالب
مروری بر تاریخچهی تابع فعال سازی
تابع فعال سازی در پرسپترون تک لایه
مروری بر تاریخچهی تابع فعال سازی
در اوایل قرن بیستم، دانشمند اسپانیایی سانتیاگو رامون ای کاخال، که اغلب پدر علوم اعصاب نامیده میشود، کشف کرد که سلولهای مغز در یک شبکه به هم پیوسته به هم متصل میشوند و در مورد نحوه ارسال سیگنالها در سیستم نظریهپردازی کرد. رامون ای کاخال جایزه نوبل فیزیولوژی یا پزشکی 1906 را با کامیلو گلگی به خاطر این کشف به اشتراک گذاشت.
در دهه 1950، دو فیزیولوژیست و بیوفیزیکدان بریتانیایی، آلن هاجکین و اندرو هاکسلی، مطالعهای بر روی آکسونها در نورونهای ماهی مرکب انجام دادند. ماهی مرکب برای تحقیقات علوم اعصاب مناسب است زیرا آکسونهای آن با چشم غیر مسلح قابل مشاهده است. محققان، ولتاژ نورونها را اندازهگیری کردند و توانستند ولتاژ مورد نیاز برای تحریک یک نورون و وادار کردن آن به انتقال سیگنال به همسایگانش را اندازهگیری کنند. ولتاژ بحرانی، پتانسیل عمل نامیده شد. بعداً به همراه همکار استرالیایی خود جان اکلس، این تیم جایزه نوبل فیزیولوژی 1963 را برای کارشان دریافت کردند.
در سال 1959، تیمی به رهبری دانشمند شناختی آمریکایی جروم یسروئل لتوین و شامل وارن مک کالوچ و والتر پیتس مقاله معروفی به نام آنچه چشم قورباغه به مغز قورباغه میگوید، منتشر کردند که در آن جزئیات چگونگی تشکیل سیستم بینایی قورباغه از شبکهای نورون های به هم پیوسته با مقادیر آستانه، به آن اجازه میدهد تا مجموعه وسیعی از توابع منطقی یا حسابی را پیاده سازی کند.
در سال 1962، روانشناس آمریکایی فرانک روزنبلات، اولین پرسپترون را با استفاده از تابع گام آستانه به عنوان یک تابع فعال سازی، و الهام گرفتن از مقالات مختلف مک کالوچ و پیتس که جداول حقیقت نورونهای بیولوژیکی را تولید کردند، توسعه داد. اکنون توابع فعال سازی از زیست شناسی به علوم اعصاب محاسباتی عبور کرده بودند.
در سال 1969، ماروین مینکسی آمریکایی و سیمور پیپرت آفریقای جنوبی کتابی با عنوان پرسپترونها: مقدمه ای بر هندسه محاسباتی منتشر کردند که محدودیتهای پرسپترون (در شکل آن زمان به عنوان یک شبکه تک لایه) را مورد بحث قرار داد. آنها اشاره کردند که به ویژه پرسپترون قادر به مدل سازی تابع XOR نیست. بدبینی آنها انگیزهای برای آغاز به اصطلاح “زمستان هوش مصنوعی” بود: دو دهه فرصتهای مالی کم تحقیقات هوش مصنوعی که تا دهه 1980 ادامه یافت، زمانی که شبکههای عصبی چند لایه محبوبیت خود را بازیافتند.
امروزه، توابع فعالسازی جزء مهمی از سیستمهای یادگیری عمیق هستند که بر تجزیه و تحلیل و تصمیمگیری در صنایع مسلط هستند. آنها شبکههای عصبی را قادر میسازند تا فراتر از افقهای باریک توابع AND، OR و NOT گسترش یابند و محققان را قادر میسازند تا با قرار دادن لایهها بر روی لایههای نورون، چسباندن به هم با توابع فعالسازی و آموزش با استفاده از الگوریتم انتشار پسانداز، به قدرت پیشبینی روزافزونی دست یابند.
ویژگیهای مهم تابع فعالسازی:
۱ـ مشکل گرادیان ناپدید:
شبکههای عصبی با استفاده ازفرآیند نزول گرادیان آموزش داده میشوند. نزول گرادیان شامل مرحله انتشار به عقب است که اساساً یک قانون زنجیرهای برای بدست آوردن تغییر در وزنها به منظور کاهش تلفات پس از هر دوره است. یک شبکه دو لایه را در نظر بگیرید که در آن لایه اول به صورت f1 (x) و لایه دوم به صورت f2 (x) نمایش داده میشود. شبکه کلی o(x) = f2(f1(x)) است. اگر وزنها را در طول انتشار رو به عقب محاسبه کنیم، o(x) = f2(x)*f1(x) بدست میآید. در اینجا f1(x) خود یک تابع ترکیبی متشکل از Act(W1x1 + b1) است که در آن Act تابع فعال سازی بعد از لایه 1 است. با اعمال مجدد قانون زنجیره، به وضوح میبینیم که f1`(x) = Act(W1x1 + b1)*x1 به این معنی که مستقیماً به مقدار فعال سازی نیز بستگی دارد.
حال تصور کنید که چنین قانون زنجیرهای در حین انتشار پس از چند لایه عبور کند. اگر مقدار Act() بین 0 و 1 باشد، چندین مقدار از این قبیل برای محاسبه گرادیان لایههای اولیه ضرب میشوند. این مقدار گرادیان را برای لایههای اولیه کاهش میدهد و آن لایهها نمیتوانند به درستی یاد بگیرند. به عبارت دیگر، شیب آنها به دلیل عمق شبکه و فعال سازی که مقدار را به صفر میبرد، از بین می روند. به این مسئله گرادیان ناپدید شدن میگویند. بنابراین ما میخواهیم تابع فعال سازی ما گرادیان را به سمت صفر تغییر ندهد.
۲ـ صفر مرکز:
خروجی تابع فعال سازی باید متقارن در صفر باشد تا شیب ها به جهت خاصی تغییر نکنند.
۳ـ هزینه محاسباتی:
توابع فعال سازی بعد از هر لایه اعمال می شوند و باید میلیون ها بار در شبکه های عمیق محاسبه شوند. بنابراین، محاسبه آنها باید از نظر محاسباتی ارزان باشد.
متمایزپذیر: همانطور که گفته شد، شبکههای عصبی با استفاده از فرآیند نزول گرادیان آموزش داده میشوند، از این رو لایههای مدل نیاز به تمایز یا حداقل متمایز شدن در بخشها دارند. این یک نیاز ضروری برای عملکرد یک تابع به عنوان لایه تابع فعال سازی است.
کاربردهای تابع فعالسازی
۱ـ توابع فعالسازی در شبکههای عصبی:
توابع فعال سازی بخش اساسی یک شبکه عصبی مصنوعی هستند. آنها یک شبکه عصبی را قادر می سازند که با چیدن لایه ها روی هم، با توابع فعال سازی به هم چسبانده شود. معمولاً هر لایه از تابعی تشکیل شده است که ورودی را در یک وزن ضرب می کند و یک بایاس اضافه می کند و به دنبال آن یک تابع فعال سازی و سپس وزن و بایاس بعدی قرار می گیرد.
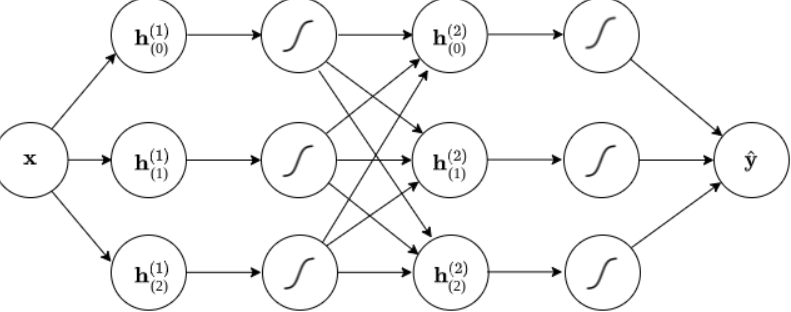
که در آن g تابع فعال سازی، W وزن در آن گره، و b بایاس است. تابع فعالسازی g میتواند هر یک از توابع فعالسازی ذکر شده تا کنون باشد. در واقع، g می تواند تقریباً هر تابع غیرخطی باشد. با توجه به اینکه g می تواند هر تابع غیرخطی باشد، راهی برای ساده سازی بیشتر این عبارت وجود ندارد. این عبارت ساده ترین شکل نمودار محاسباتی کل شبکه عصبی را نشان می دهد. یک شبکه عصبی ساده مانند این قادر است بسیاری از توابع پیچیده منطقی یا حسابی مانند تابع XOR را یاد بگیرد.
بنابراین، یک شبکه عصبی بدون توابع فعال سازی معادل یک مدل رگرسیون خطی است و نمی تواند عملیات پیچیده تر از مدل سازی خطی را انجام دهد. به همین دلیل، تمام شبکه های عصبی مدرن از نوعی تابع فعال سازی استفاده می کنند.
تابع فعال سازی در پرسپترون تک لایه
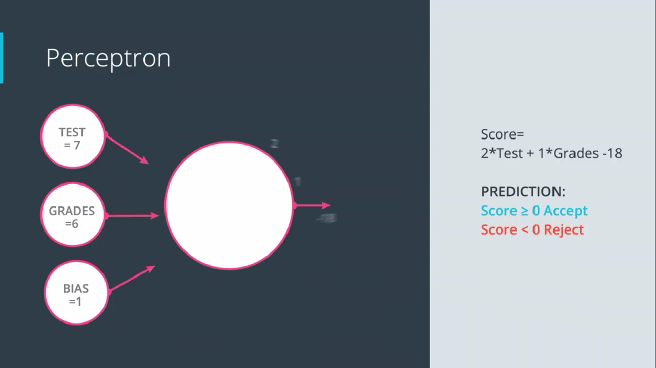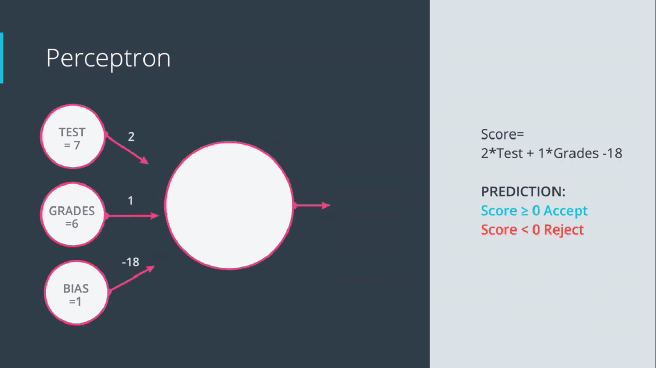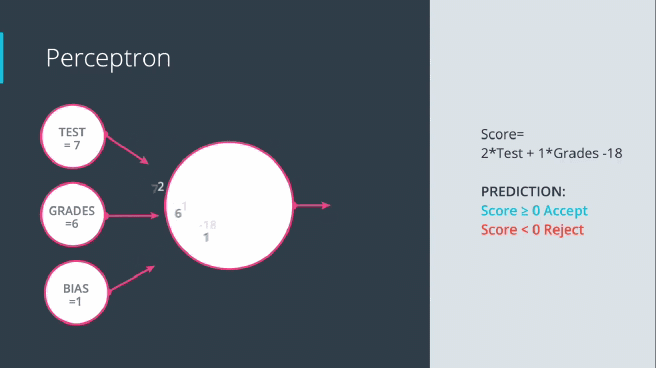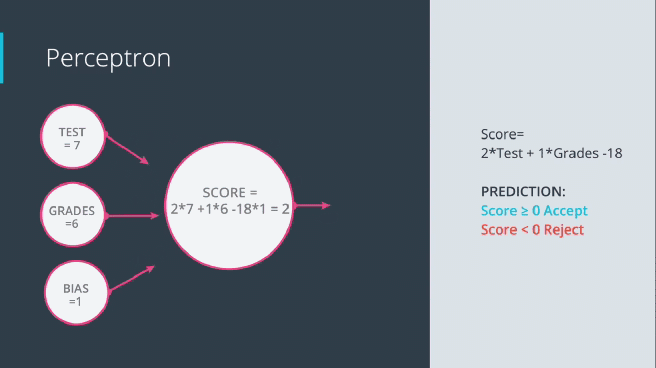
با در نظر گرفتن مفهوم تابع فعال سازی با توجه به سادهترین اصول اولیه، یک نورون منفرد در یک شبکه عصبی و به دنبال آن یک تابع فعال سازی میتواند به عنوان یک دروازه ورود اطلاعات رفتار کند. تابع مرحله آستانه را به عنوان تابع فعال سازی خود در نظر بگیرید:
تعریف ریاضی تابع گام آستانه، که یکی از سادهترین توابع فعال سازی ممکن است به شرح زیر است:
تابع مرحله آستانه ممکن است اولین تابع فعال سازی باشد که توسط فرانک روزنبلات در حالی که در سال 1962 در حال مدل سازی نورونهای بیولوژیکی بود، معرفی شد.
یک شبکه عصبی تک لایه را که پرسپترون تک لایه نیز نامیده می شود، به صورت زیر تعریف کنیم:
(فرمول و نمودار محاسباتی یک پرسپترون تک لایه ساده با دو ورودی)
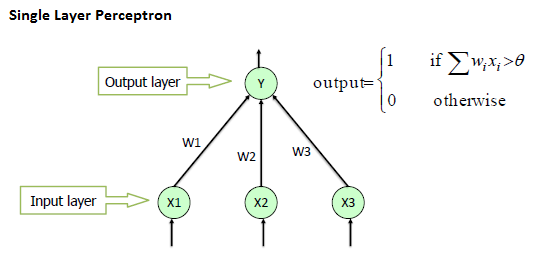
برای ورودیهای باینری 0 و 1، این شبکه عصبی میتواند رفتار تابع OR را بازتولید کند. جدول آن به شرح زیر است:

با اضافه کردن وزن ها و بایاس ها، ساختن پرسپترون برای محاسبه توابع OR، AND یا NAND بسیار آسان است. این کشف یکی از اولین رویدادهای مهم در توسعه شبکههای عصبی مصنوعی بود و به محققان اولیه هوش مصنوعی سرنخی داد که وزنها، سوگیریها و توابع فعالسازی را میتوان به گونهای با الهام از شبکههای عصبی بیولوژیکی ترکیب کرد و باعث ایجاد نوعی هوش مصنوعی. با این حال، یک محدودیت مهم وجود دارد که به طور مشهور توسط مینسکی و پیپرت در سال 1969 برجسته شد: هیچ راهی برای به دست آوردن یک پرسپترون تک لایه برای اجرای تابع XOR وجود ندارد، مهم نیست که چه وزنها و سوگیریهایی انتخاب شدهاند. اگر دو ورودی متفاوت باشند، تابع XOR عدد 1 و اگر مساوی باشند 0 را برمیگرداند.

برای دستیابی به عملیات پیچیده تر مانند تابع XOR، حداقل به دو لایه نیاز است. در واقع، یک شبکه عصبی تنها از دو لایه، به شرطی که دارای یک تابع فعال سازی باشد، قادر به پیاده سازی هر تابع ممکن است، نه فقط XOR. دو دهه طول کشید تا حوزه شبکه های عصبی از این نقطه گیر پیشرفت کند. این نشان میدهد که عملکرد فعالسازی چقدر قدرتمند است، اما پتانسیل واقعی آن تنها زمانی قابل تحقق است که به عنوان چسب در یک شبکه عصبی چند لایه استفاده شود.
سخن آخر
امروزه، توابع فعالسازی جزء مهمی از سیستمهای یادگیری عمیق هستند که بر تجزیه و تحلیل و تصمیمگیری در صنایع مسلط هستند. آنها شبکههای عصبی را قادر میسازند تا فراتر از افقهای باریک توابع AND، OR و NOT گسترش یابند و محققان را قادر میسازند تا با قرار دادن لایهها بر روی لایههای نورون، چسباندن به هم با توابع فعالسازی و آموزش با استفاده از الگوریتم انتشار پسانداز، به قدرت پیشبینی روزافزونی دست یابند. برای یادگیری بیشتر دربارهی توابع فعالسازی در شبکههای عصبی پیشنهاد میکنم به آموزش توابع فعالسازی در پرتال هوش مصنوعی سر بزنید. امیدوارم این مطلب برای شما مفید بوده باشد.